Converting Finite Automata to Regular Expression using Arden’s Theorem
The Arden’s Theorem can be applied to find the regular expression recognized by the given transition diagram. This theorem can be applied to transition diagram not containing ε-moves or ε-transitions. Let’s first understand the Arden’s Theorem.
Arden’s Theorem
Let P, Q, and R be three Regular Expressions over ∑. If P does not contain ε then the equation R= Q + RP has a unique solution given by R = QP*
Proof:
We have R = Q + RP* ……….Eq (1)
and R = QP*
Substitute R = QP* in (1) we get.
R = Q + (QP*) P
= Q + QP*P
= Q (ε + P*P)
= QP* (by using identity ε + R*R = R*)
Thus R = QP* is a solution of R = Q + RP
Example 1
Find the regular expression equivalent to the following transition diagram.

Solution:
The above transition diagram does not contain ε-moves or transitions. So, we apply Arden’s Theorem method to find the regular expression.
The equation corresponding to state q0 and q1 is shown below:
q0 = q0b + ε …………. (1)
q1 = q0a + q1a + q1b ……………… (2)
In given transition diagram q1 is the final state. So, the resulting regular expression will be equal to q1.
From eq (2) we have:
q1 = q0a + q1a + q1b
q1 = q0a + q1 (a + b)
q1 = q0a (a + b)*
(by using Arden’s Theorem, if R = Q + RP then R = QP* ) ……………… (3)
From equation (1), we have
q0 = q0b + ε
q0 = εb*
q0 = b* (using Arden’s Theorem)
Substituting the value of q0 = b* in equation (3) we get,
q1 = b*a (a + b)*
Hence the final Regular Expression equivalent to the given transition diagram is:
Regular Expression = b*a (a + b)*.
Example 2
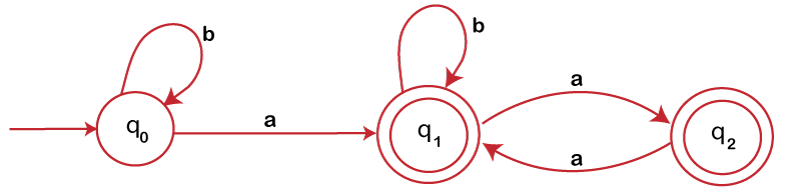
Find the regular expression equivalent to the following transition diagram.
Solution:
The above transition diagram does not contain ε-moves or transitions. So, we apply Arden’s Theorem method to find the regular expression.
The equations corresponding to state q0, q1 and q2 is shown below:
q0 = q0b + ε …………. (1)
q1 = q0a + q1b + q2a ……………… (2)
q2 = q1a ……………… (3)
In given transition diagram, q1 and q2 are the final states. So, the final resulting regular expression will be equal to the sum of both the regular expressions.
From equation (1), we have
q0 = q0b + ε
q0 = εb*
q0 = b* (using Arden’s Theorem)
Substituting the value of q0 and q2 in equation (2), we get ………………….. (4)
q1 = q0a + q1b + q2b a
q1 = b*a + q1b + q1aa
q1 = b*a + q1 (b + aa)
q1 = b*a (b + aa)* …………………… (5)
Substituting the value of q1 from equation (5) to equation (3), we get
q2= q1a
q2 = b*a (b + aa)*a
Hence the final Regular Expression equivalent will be equivalent to:
Regular Expression = q1 + q2 = b*a (b + aa)* + b*a (b + aa)*a
Example 3
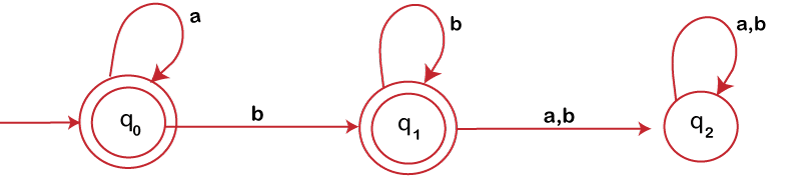
Find the regular expression equivalent to the following transition diagram.
Solution:
The above transition diagram does not contain ε-moves or transitions. So, we apply Arden’s Theorem method to find the regular expression.
The equations corresponding to state q0, q1 and q2 is shown below:
q0 = q0a + ε …………. (1)
q1 = q0b + q1b ……………… (2)
q2 = q1 (a +b) + q2 (a + b) ……………… (3)
In given transition diagram q0 and q1 are the final state. So, the final resulting regular expression will be equal to the sum of both the regular expressions.
From equation (1), we have
q0 = q0a + ε
q0 = ε a*
q0 = a* (using Arden’s Theorem) ………………….. (4)
by substituting the value of q0 in equation (2), get
q1 = q0b + q1b
q1 = a*b + q1b
q1 = a*bb*
q0 + q1 = a* + a*bb*
= a*(ε + bb*)
= a*b* ( by using identity ε + RR* = R*)
Hence the final Regular Expression equivalent to the given transition diagram is
Regular Expression = a*b*.

